Some things, like the "self-operated napkin", are just too complicated!

Do we really need over 100,000 free parameters to build a good MNIST classifier? It turns out that we can eliminate 50-90% of them.

How many parameters is enough?

The fruit fly was to genetics what the MNIST dataset is to deep learning: the ultimate case study. The idea is to classify handwritten digits between 0 and 9 using 28x28 pixel images. A few examples of these images are shown:

Examples taken from the MNIST dataset.

Ughh, not MNIST tutorials again. There is an endless supply of tutorials that describe how to train an MNIST classifier. Looking over them recently, I noticed something: they all use a LOT of parameters. Here are a few examples:

Author Package Type Free params Test acc.
TensorFlow TF FC 7,850 92%
PyTorch PyTorch CNN 21,840 99.0%
Elite Data Science Keras CNN 113,386 99\(^+\)%
Machine Learning Mastery Keras CNN 149,674 98.9%
Lasagne Lasagne CNN 160,362 99\(^+\)%
Caffe Caffe CNN 366,030 98.9%
Machine Learning Mastery Keras FC 623,290 98%
Lasagne Lasagne FC 1,276,810 98-99%
Tensorflow TF CNN 3,274,625 99.2%

It would seem that you have two options: use a small number of weights and get low accuracy (TensorFlow’s logistic regression example) or use 100,000\(^+\) weights and get 99\(^+\)% accuracy (the PyTorch example is a notable exception). I think this leads to a common misconception that the best way to gain a few percentage points in accuracy is to double the size of your model.

MNIST lite. I was interested in how slightly smaller models would perform on the MNIST task, so I built and trained a few:

Package Structure Type Free params Test accuracy
PyTorch 784 \(\mapsto\) 16 \(\mapsto\) 10 FC 12,730 94.5%
PyTorch 784 \(\mapsto\) 32 \(\mapsto\) 10 FC 25,450 96.5%
PyTorch 784 \(\mapsto\) (6,4x4) \(\mapsto\) (6,4x4) \(\mapsto\) 25 \(\mapsto\) 10 CNN 3,369 95.6%
PyTorch 784 \(\mapsto\) (8,4x4) \(\mapsto\) (16,4x4) \(\mapsto\) 32 \(\mapsto\) 10 CNN 10,754 97.6%

You can find the code on my GitHub. As you can see, it’s still possible to obtain models that get 95\(^+\)% accuracy with fewer than 10\(^4\) parameters. That said, we can do even better…

Optimizing subspaces

“Make everything as simple as possible, but not simpler.” – Albert Einstein

The trick. When I interviewed with anonymous at anonymous earlier this year, we discussed the idea of optimizing subspaces. In other words, if the vector \(\theta\) contains all the parameters of a deep network, you might define \(\theta = P \omega\) where the vector \(\omega\) lives in some smaller-dimensional space and \(P\) is a projector matrix. Then, instead of optimizing \(\theta\), you could optimize \(\omega\). With this trick, we can choose an arbitrary number of free parameters to optimize without changing the model’s architecture. In math, the training objective becomes:

\[\begin{align} \omega &= \arg\min_{\mathbf{\omega}} -\frac{1}{n} \sum_X (y\ln \hat y +(1-y)\ln (1-\hat y))\\ &\mathrm{where} \quad \hat y = f_{NN}(\theta, X) \quad \mathrm{and} \quad \theta = P \omega \end{align}\]

If you want to see this idea in code, check out my subspace-nn repo on GitHub.

Results. I tested this idea on the model from the PyTorch tutorial because it was the smallest model that achieved 99\(^+\)% test accuracy. The results were fascinating.

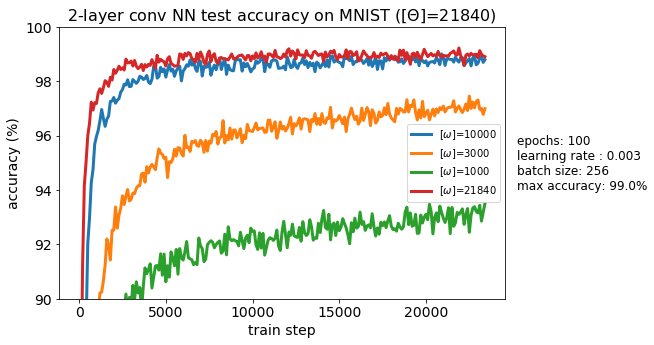
As shown below, cutting the number of free parameters in half (down to 10,000 free parameters) causes the test accuracy to drop by only 0.2%. This is substantially better than the “MNIST lite” model I trained with 10,754 free parameters. Cutting the subspace down to 3,000 free parameters produces a test accuracy of 97% which is still pretty good.

Framework Free parameters Test accuracy
PyTorch 21,840 99.0%
PyTorch 10,000 98.8%
PyTorch 3,000 97.0%
PyTorch 1,000 93.5%

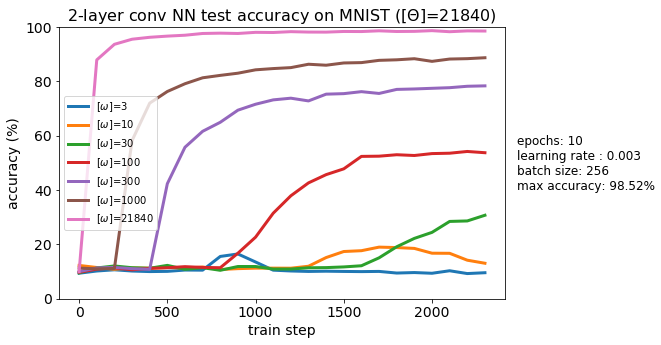
Ultra small subspaces. We can take this idea even futher and optimize our model in subspaces with well below 1,000 parameters. Shown below are test accuracies for subspaces of size 3, 10, 30, 100, 300, and 1000. Interestingly, I tried the same thing with a fully connected model and obtained nearly identical curves.

Performing optimization in very small subspaces. Some of these training trajectories have not reached convergence; the 1,000-parameter model, for example, will converge to 93.5% accuracy after several more epochs.

Takeaways

Update. My friend, (anonymous), just finished a paper about this. Much more #rigorous than this post and definitely worth checking out: “solving the cart-pole RL problem is in a sense 100 times easier than classifying digits from MNIST.”

Literature. The idea that MNIST classifiers are dramatically overparameterized is not new. The most common way to manage this issue is by adding a sparsity term (weight decay) to the loss function. At the end of the day, this doesn’t exactly place a hard limit on the number of free parameters. One interesting approach, from Convolution by Evolution\(^\dagger\), is to evolve a neural network with 200 parameters. The authors used this technique to train a denoising autoencoder so it’s difficult to directly compare their results to ours.

There are several other papers that try to minimize the number of free parameters. However, I couldn’t find any papers that used the subspace optimization trick. Perhaps it is a new and interesting tool.

Bloat. The immediate takeaway is that most MNIST classifiers have parameter bloat. In other words, they have many more free parameters than they really need. You should be asking yourself: is it worth doubling the parameters in a model to gain an additional 0.2% accuracy? I imagine that the more complex deep learning models (ResNets, VGG, etc.) also have this issue.

Training a model with more parameters than you’ll need is fine as long as you know what you’re doing. However, you should have a general intuition for how much parameter bloat you’ve introduced. I hope this post helps with that intuition :)

      \(^\dagger\)Parts of this paper are a little questionable…for example, the ‘filters’ they claim to evolve in Figure 5 are just circles.