Self-classifying MNIST Digits

In this project, we treat every pixel in an image as a biological cell. Then we train these cells to send signals to their neighbors so that, over time, the entire population will agree on what digit they are shaping. Every cell “votes” on the global shape by turning one of ten different colors, corresponding to the ten digits. Sometimes the truth prevails and sometimes they are collectively misguided. I like @hardmaru’s example, reproduced below, of a 4 vs. a 2 (🔴 🔵). It’s similar to an election process – it even has “swing states:”

I encourage you to read the article and try the interactive demo for yourself on Distill:

Useful properties of Cellular Automata

One of the takeaways from helping write this Distill article is that cellular automata are fascinating and underrated. In particular, I like them because they are:

Local. All interactions in physics are local – aside from quantum entanglement, and even that is up for debate.¹ All interactions in chemistry and biology are also local, including the interactions between neurons that allow us to learn. The value of locality is that it is one of the strongest bounds on the complexity of a system. Without locality, any unit (atom, molecule, cell, human) can interact with any other, leading to an exponential growth in causal influences on each unit as the size of the system increases. This is bad news if you want to establish any interesting chains of causality between various sub-units.² For example, when you store information using a small chunk of matter, you do so under the assumption that that information will remain where it is and not change in response to external factors.

Parallelizable. One particularly important advantage of locality is that it makes CAs immensely parallelizable. It’s not hard to train or evaluate a large population of CAs asynchronously: disparate parts of the system never have to communicate or synchronize with one another. This is why, if we do live in a simulation, it is probably implemented with a CA.³

Scalable in number of cells. This is closely connected to “parallelizable.” Imagine training a 20x20 population of cells to do something and then running a 200x200 population of them on some downstream task. The numbers are different, but we actually do this in the demo. This is not something you can do with neural networks.

Expressive. Given how simple some CAs can be – for example, Conway’s Game of Life – they have impressive theoretical properties. They are Turing complete and can simulate any other system. You could even use Conway’s Game of Life to simulate Conway’s Game of Life…and yes, someone actually did this.

Resilient. Systems where local interactions eventually lead to global behavior are extraordinarily resilient. You can cut a 2-headed planarian in half and both halves will regenerate. You can cut a limb from a tree and the tree will survive. You can leave your company and your coworkers will continue on without you, barely noticing your absence. Ok, that was a joke, they will miss you, but in theory they should be able to cover for you when you take a few vacation days.

Likely to fail gracefully. It’s hard to define what it means to “fail gracefully” so this last point is a bit subjective. Consider the failure case of the 4/2 pattern from the video above, reproduced below. That shape is far outside of the CA’s training distribution, but it responded in a fairly intuitive manner. On the left is another fun failure case where a CA was trained to grow, from a single cell, into a yellow fish emoji. The population of cells kept growing even after it became a mature fish, but did so in a way that preserved the fish’s shape and body texture.

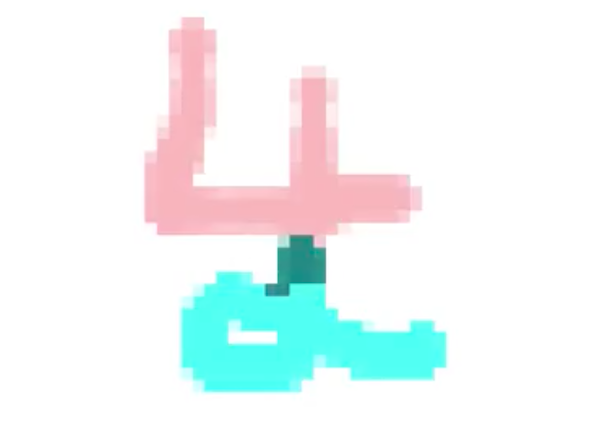
I like CA as a design motif. They capture a set of elegant design principles that, even if we don’t follow them strictly at all times in other areas of science, are worth thinking about.

Parting words

It feels good to have released the Distill article and demo to the world. Now, on thousands of different browser screens, our little cells are coming to life. They are looking at their particular MNIST pixels, talking to their neighbors, and trying to figure out what their overall digit shape is. Little do they know, they are part of a human scientific endeavor that is much the same. For we humans, too, are looking at our local surroundings, talking with our neighbors, and trying to agree on the overall shape of our reality.

Best of luck to the little cells and to us humans as well.

Footnotes