Studying Growth with Neural Cellular Automata

How does a single fertilized egg grow into a population of seventy trillion cells: a population that can walk, talk, and write sonnets? This is one of the great unanswered questions of biology. We may never finish answering it, but it is a productive question nonetheless. In asking it, scientists have discovered the structure of DNA, sequenced the human genome, and made essential contributions to modern medicine.

In this post, we will explore this question with a new tool called Neural Cellular Automata (NCA).

Motivation

The purpose of cellular automata (CA) writ large is to mimic biological growth at the cellular level. Most CAs begin with a grid of pixels where each pixel represents a different cell. Then a set of growth rules, controlling how cells respond to their neighbors, are applied to the population in an iterative manner. Although these growth rules are simple to write down, they are choosen so as to produce complex self-organizing behaviors. For example, Conway’s Game of Life has just three simple growth rules that give rise to a diverse range of structures.¹

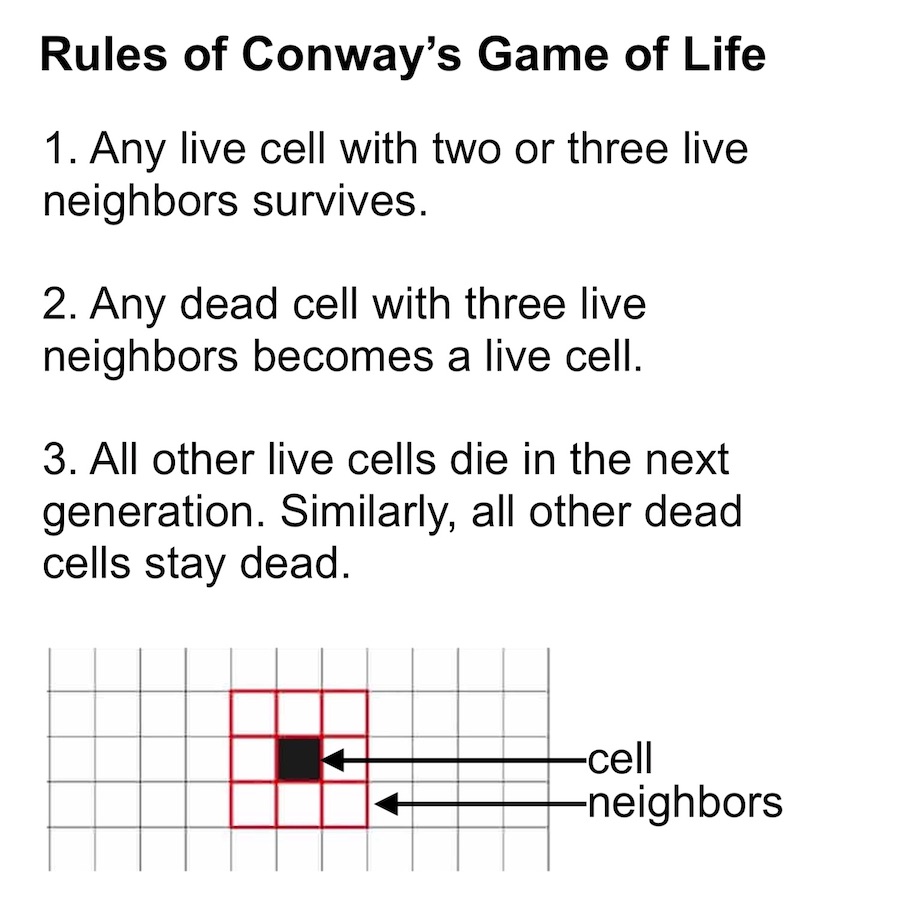
Classic versions of cellular automata like Conway’s Game of Life are interesting because they produce emergent behavior starting from simple rules. But in a way, these versions of CA are too simple. Their cells only get to have two states, dead or alive, whereas biological cells get to have a near-infinite number of states, states which are determined by a wide variety of signaling molecules. We refer to these molecules as morphogens because they work together to control growth and guide organisms towards specific final shapes or morphologies.

Neural CA. Based on this observation, we should move away from CA with cells that are only dead or alive. Instead, we should permit their cells to exist in a variety of states with each state defined by a list of continuous variables. Growth rules should operate on combinations of these variables in the same way that biological growth rules operate on combinations of different morphogens. And unlike Conway’s Game of Life, the self-organizing behaviors that arise should not be arbitrary or chaotic. Rather, they should involve stable convergence to specific large-scale morphologies like those that occur in biology. Much more complex growth rules are needed for this to occur.

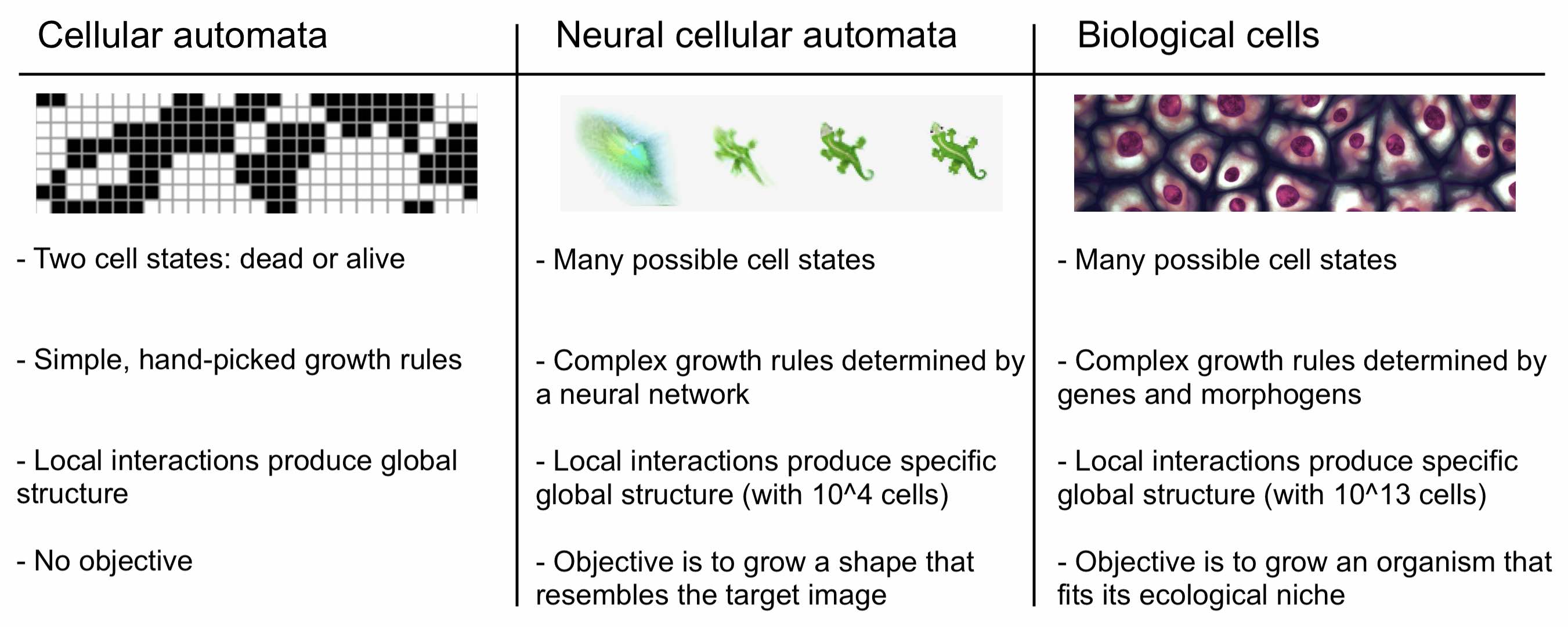
The diagram above shows how NCA take a step in the right direction. Unlike regular cellular automata, they represent each cell state with a real-valued \(n\)-dimensional vector and then allow arbitrary growth rules to operate on that domain. They do this by parameterizing growth rules with a neural network and then optimizing the neural network to obtain the desired pattern of growth. To showcase the model’s expressivity, the authors trained it to arrange a population of a 1600 cells in the shape of a lizard starting from local-only interactions between initially identical cells.

NCA diagram. The diagram above how a neural network can be used to parameterize the growth rules of a cellular autiomata. The original NCA article uses this diagram to introduce the model and its training procedure.

Getting started

The authors of the original paper released a Colab notebook that showed how to implement NCA in TensorFlow. Starting from this notebook, we reimplemented everything in PyTorch and boiled it down to a minimalist, 150-line implementation. Our goal was to make the NCA model as simple as possible so that we could hack and modify it without getting overwhelmed by implementation details.

Having implemented our own NCA model, the next step was to scale it to determine the maximum size and complexity of the “organisms” it could produce. We found that the population size was going to be limited by the amount of RAM available on Google Colab GPUs. We maxed things out with a population of about 7500 cells running for about 100 updates. For context, the original paper used a population of 1600 cells running for 86 updates.

Working in this scaled-up regime, we trained our NCA to grow a number of different flowers. Some of the early results were a bit mangled and blurry. Many were biased towards radial symmetry and required extra training in order to reveal symmetric features such as individual petals. But soon, after a few hyperparameter fixes, our NCA was able to grow some “HD” 64x64 flowers:

Having implemented the NCA model and gained some intuition for how it trained, we were ready to use it to investigate patterns of biological growth.

Patterns of biological growth

Biological growth is wonderfully diverse. Consider this passage from the first chapter of Growth by Life Science Library:

A eucalyptus native to Uganda has been known to grow 45 feet in two years, whereas dwarf ivy generally grows one inch a year. The majestic sequoia of California, which starts out as a seed weighing only one three-thousandth of an ounce, may end up… [with a] weight estimated at 6,200 tons. It takes more than 1,000 years for the sequoia to achieve the feat of multiplying 600 billion times in mass.

The animal kingdom, too, has its champions of growth. The blue whale, which cruises the oceans from the North to the South Pole, begins life as a barely visible egg weighing only a fraction of an ounce. At birth, it weighs from two to three tons. When it is weaned, at about seven months, it is 52 feet long and weighs 23 tons, having gained an average of 200 pounds a day.

Given the diversity of life forms on our planet, maybe one of the biggest surprises is how much they have in common. For the most part they share the same genetic materials, signaling mechanisms, and metabolic pathways. Their cells have the same life cycles. Indeed, the cellular mechanics in a gnat look pretty similar to those in a blue whale…even though the creatures themselves could not be more different.

1. Gnomonic growth

One shared pattern of growth is called gnomonic growth. This pattern tends to occur when an organism needs to increase in size and part of its body is defined by a rigid structure. You can see this in clams, for example. Their shells are rigid and cannot be deformed. And yet they need to grow their shells as the rest of them grows. Clams solve this problem by incrementally adding long crescent-shaped lips to the edges of their shells. Each new lip is just a little larger than the one that came before it. These lips, or gnomons as they are called, permit organisms to increase in size without changing form. Gnomons also appear in horns, tusks, and tree trunks.

One of the most famous products of gnomonic growth is the nautilus shell. In this shell, the gnomons grow with such regularity that the overall shape can be modeled with a simple Fibonacci sequence. The elegance and simplicity of the pattern makes it an interesting testbed for NCA.

To set up this problem, we split the shell into three regions: frozen, mature, and growing. These regions are shown in cyan, black and magenta respectively:

The cells in the frozen region are, as the name would suggest, frozen. Both their RGBA and hidden channels are fixed throughout training. The cells in the mature region are similar; the only difference is that their hidden channels are allowed to change. The growing region, meanwhile, begins the simulation without any living cells. Cells from the mature region need to grow outwards into this area and arrange themselves properly before the simulation ends.

Scale and rotation invariance. Part of the objective in this “gnomonic growth” problem is to learn a growth rule that is scale and rotation invariant. We can accomplish this by rotating and scaling the nautilus template as shown in the six examples above. By training on all of these examples at once, we are able to obtain a model that grows properly at any scale or orientation. Once it learns to do this, it can grow multiple gnomons, one after the other, without much interference. Below, for example, we add eight new compartments and quadruple the shell’s size by letting the NCA run for eight growth cycles.²

One of the things that makes this growth pattern interesting is that the NCA cells have to reach a global consensus as to what the scale and rotation of the mature region is. Only by agreeing on this are they able to construct a properly-sized addition. And yet in practice, we see that expansion into the growth region begins from the first simulation step. This suggests that cells in the mature region try to come to a distributed consensus as to the target shape even as new cells are already beginning to grow that shape. Once cells in the mature region know the proper scale and rotation of the gnomon, they transmit this information to the growing region so that it can make small adjustments to its borders. If you look closely, you can see these adjustments happening in the video below.

This process of reaching a consensus in a decentralized and asynchronous manner is a common problem for biological cells. In fact, we already touched on it in our Self-classifying MNIST Digits post. It’s also important in human organizations: from new cities agreeing on development codes, to democratic institutions agreeing on legislation, to the stock market agreeing on how to value companies. It is not always a low-entropy process.

Indeed, sometimes groups of cells have to resort to other means of reaching consensus…

2. Embryonic induction

The alternative to a fully decentralized consensus mechanism is cellular induction. This happens when one small group of cells (usually in an embryo) tells the rest how to grow. The first group of cells is called the inducing tissue and the second is called the responding tissue. Induction controls the growth of many tissues and organs including the eye and the heart.

In this section, we will grow an image of a newt and then graft part of its eye tissue onto its belly. After doing this, we will watch to see whether those cells are able to induce growth in the rest of the eye in that region. We’ve chosen this particular experiment as an homage to Hans Spemann,³ who won the Nobel Prize for Medicine in 1935 for using similar experiments on real newts to discover “the organizer effect in embryonic development.”⁴ Spemann’s major insight was that “at every stage of embryonic development, structures already present act as organizers, inducing the emergence of whatever structures are next on the timetable.”⁵

To reproduce this effect, we first trained an NCA to grow a picture of a newt. Once the growth phase was complete, we grafted a patch of cells from its head onto its stomach. This patch of cells included the upper, light-colored portion of the newt’s eye but not the dark-colored, lower portion. Then we froze their states and allowed the rest of the cells to undergo updates as usual. Within 25 steps, the stomach cells below the grafted patch had regrown into a dark-colored strip to complete the lower half of the new eye.

Cellular induction offers a simple explanation for how many growth rules are implemented: by and large, they are implemented as if-then statements. For example, “If I am growing below some light-colored eye tissue, then I should be black-colored eye tissue.” Early in embryonic development, these if-then statements are very general: “If I am on the outside layer of the embryo, then I am going to be an ectoderm cell. Else, if I am on the inside layer of the embryo, then I am going to be a mesoderm cell. Else, if I am in the center of the embryo, then I am going to be an endoderm cell.”

As development progresses, these branching milestones occur dozens of times, each time causing a group of cells to become more specialized. Towards the end of development, the branching rules might read, “If I am an ectoderm cell and if I am a nervous system cell and if I am an eye cell and if I am distal to the optic nerve then I am going to be part of the corneal epithelium.”

Attractor theory of development. While this sounds complex, it’s actually the simplest and most robust way to construct a multicellular organism. Each of these branching statements determines how morphogenesis unfolds at a different hierarchy of complexity. Unlike a printer, which has to place every dot of ink on a page with perfect precision, a growing embryo doesn’t need to know the final coordinates of every mature adult cell. Moreover, it can withstand plenty of noise and perturbations at each stage of development and still produce an intricate, well-formed organism in the end.⁶ Intuitively, this is possible because during each stage of growth, clusters of cells naturally converge to target “attractor” states in spite of perturbations. Errors get corrected before the next stage of growth begins. And in the next stage, new attractor states perform error-correction as well. In this way, embryonic induction allows nature to construct multicellular organisms with great reliability, even in a world full of noise and change.

3. Apoptosis

Death to form the living. One of the most dramatic if-then statements is “If I am in state x, then I must die.” This gives rise to what biologists call apoptosis, or programmed cell death. Apoptosis is most common when an organism needs to undergo a major change in form: for example, a tadpole losing its tail as it grows into a frog, or a stubby projection in a chick embryo being sculpted into a leg.

Left. The metamorphosis of a tadpole into a frog is a spectacular example of apoptosis. Soon after the tadpole's tail reaches full size, the frog's back legs begin to grow and the tail rapidly shrinks. In the span of a few months it vanishes entirely. Right. A blue dye that stains only dead cells is applied to a four-year-old chick embryo, revealing apoptosis in the wing and foot buds. These cells are programmed to die at an appointed time in order to shape the wings and feet of the newborn chick (see white circles). Even if these cells are moved to another part of the embryo, they still die at the appointed time. Photo credit: Growth from the LIFE Science Library.

One of the best examples of apoptosis in the human body is bone remodeling. This is the process by which bones grow, change shape, and even regrow after a fracture. It’s also a process by which the body manages the supply of important minerals and nutrients such as calcium. In the first year of life, bone resorption proceeds at an especially rapid pace. By the end of that year, almost 100% of the skeleton has been absorbed and replaced.

Even in adults, about 10% of the skeleton is replaced every year.

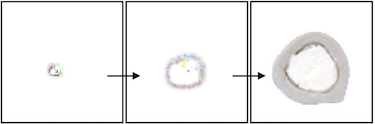
In this experiment, we trained an NCA model to grow into the shape of a slice of human bone. Since the bone starts its growth in the center of the image, but the center of the target image is empty, the NCA naturally learns a growth pattern that resembles apoptosis. Early in development, a small tan circle forms. The outside edge of this circle expands rapidly outward in a pattern of “bone growth” that would be carried out by osteoblasts in nature. Meanwhile, the inside edge of the circle deteriorates at the same rate in a pattern of “bone resorption” associated with osteoclasts in nature.

4. Speciation

We have remarked that gnats and blue whales have more in common, at least in terms of cellular mechanics, than one would guess. They share many of the same cell structures, protiens, and even stages of development like gastrulation. This points to the fact that many different organisms share the same cellular infrastructure. In more closely-related species, this observation is even more apt. For example, the three flowers we grew at the beginning of the article – the rose, the marigold, and the crocus – are all angiosperms and thus share structures like the xylem and phloem.

Indeed, one of the biggest differences between these flowers is their genetic code. Making an analogy to computers, you might say that they have the same hardware (cell mechanics), but different software (DNA).

Our final experiment uses NCA to explore this idea. We run the same cellular dynamics (NCA neural network weights) across several flowers while varying the genetic information (initial state of the seed cell). Our training objective involved three separate targets: the rose, the marigold, and the crocus, each with its own trainable “seed state.” Early in training, our model produced blurry flower-like images with various mixtures of red, yellow, and purple. As training progressed, these images diverged from one another and began to resemble the three target images.

Even though the final shapes diverge, you can still see shared features in the “embryonic” versions of the flowers. If you watch the video below, you can see that the three “embryos” all start out with red, yellow, and purple coloration. The developing crocus, in particular, has both red and purple petals during growth steps 10-20.

From a dynamical systems perspective, this NCA model has three different basins of attraction, one for each flower. The initial seed determines which basin the system ultimately converges to. In the future, it would be interesting to train a model that produces a wider variety of final organisms. Then we could use its “DNA” vectors to construct a “tree of life,” showing how closely-related various organisms are⁷ and at what point in training they split from a common ancestor.

Final remarks

There are a number of ways that NCA can contribute to civilization. The prospect of isolating the top one hundred signaling molecules used in natural morphogenesis, tracking their concentrations during growth in various tissues, and then training an NCA to reproduce the same growth patterns with the same morphogens is particularly exciting. This would allow us to obtain a complex model of biological morphogenesis with some degree of predictive power. Such a model could allow us to solve for the optimal cocktail of signaling molecules needed to speed up, slow down, or otherwise modify cell growth. It could even be used to adversarially slow down the growth of cancerous cells in a patient with cancer or artificially accelerate the growth of bone cells in a patient with osteoporosis.

One of the themes of this post is that patterns of growth are surprisingly similar across organisms. This hints at the fact that there are principles of growth that transcend biology. These principles can be studied in a computational substrate in a way that gives useful insights about the original biological systems. These insights, we believe, shine a new light on the everyday miracle of growth.

Footnotes