Differentiable Memory and the Brain

DeepMind’s Differentiable Neural Computer (DNC) represents the state of the art in differentiable memory models. I introduce an analogy between the DNC and human memory, then discuss where it breaks down.

Introduction

Motivation. Neural networks represent the state of the art in computer vision, translation, and artificial intelligence. They are also of interest to neuroscientists because they perform computations in much the same way as the human brain. In recent years, researchers have introduced several neural-network based models that can read and write to external memory in a fully differentiable manner.

Roadmap. Here I explore one of these models, the Differentiable Neural Computer (DNC), through the lens of human memory research. Using the free recall task, I test an analogy between the DNC and the Temporal Context Model of human memory. My results indicate similar primacy and recency effects but suggest a breakdown of the analogy around mechanisms of forgetting and context storage.

The king of differentiable memory

Differentiable memory. Neural networks perform well over a broad range of pattern recognition tasks. Recurrent Neural Networks (RNNs), a subtype of these models, can solve sequence modeling tasks such as translation, handwriting generation, and speech recognition by storing ‘world states’ in a memory vector^{1 2 3}. Unfortunately, the computational cost of RNNs scales poorly with memory size. This prevents them from storing rich information about their environments over very long timescales.

To solve this problem, researchers have proposed a variety of interfaces between neural networks and large external memories^{4 5 6 7}. The idea is to train an RNN to read and write ‘memory vectors’ on a large memory matrix \(M\). These models are fully differentiable and can be trained end-to-end with gradient descent, so researchers sometimes refer to them as differentiable memory models. The most advanced differentiable memory model is the Differentiable Neural Computer (DNC). Researchers at Google DeepMind described this model in a 2016 paper in Nature⁴, where they used it to navigate the London Underground, solve reinforcement learning puzzles, and attain state-of-the-art performance on the challenging bAbi dataset.

Implementing the DNC. I wrote a batched version of the DNC in TensorFlow 1.0, working directly from the equations in the appendix of the Nature paper⁴. My code is on GitHub. To make sure everything was working correctly, I replicated the repeat-copy task results in the paper’s appendix.

The DNC achieves perfect performance on the repeat-copy task

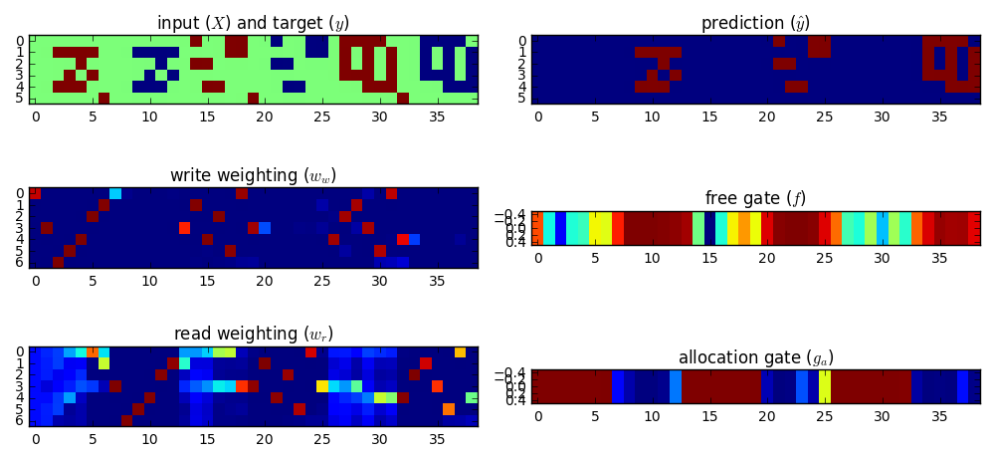
Introducing the DNC-brain analogy

“The DNC can thus learn to plan routes on the London Underground, and to achieve goals in a block puzzle, merely by trial and error—without prior knowledge or ad hoc programming for such tasks.” – DNC Nature article, Editor’s Summary

Using Michael Kahana’s college textbook, Foundations of Human Memory, I will explain how the DNC schema uses five key human memory concepts:

1. Attribute theory
2. Similarity measures
3. Search of Associative Memory (SAM)
4. Temporal Context Model (TCM)
5. Serial recall

1. Attribute theory. In attribute theory, each memory is represented by a list of attribute values, one value for each attribute^{8 9}. These attributes describe both the memory and the context in which it was formed. We can concatenate these values together to form attribute vectors. In fact, Heusser et al (Heusser 2017)¹⁰ built attribute vectors from human fMRI data and used them to explore the human ‘memory space’ (Manning 2017)¹¹.

The DNC also uses vectors to store memories. Each row of the memory matrix \(M \in \mathbb{R}^{N \times W}\) (part c in the figure below) corresponds to a different memory⁴. If \(E \in \mathbb{R}^{N \times W}\) is a matrix of ones, \(w \in \mathbb{R}^N\) is a normalized vector of write weights, \(\mathbf{v} \in \mathbb{R}^W\) is a new memory, and \(\mathbf{e} \in \mathbb{R}^W\) is an erase vector, then the DNC’s memory matrix can be updated with

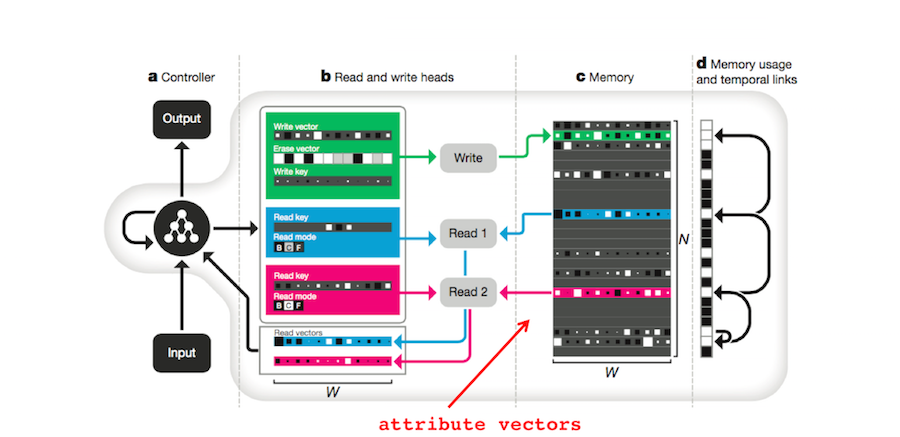
2. Similarity measures. In Foundations of Human Memory⁸, Kahana introduces the summed similarity model to explain results from Hintzman and Block (1971)⁹. The model uses a similarity measure (e.g. cosine similarity) to determine whether a probe vector matches a set of memory vectors. The idea is that the brain might use a related similarity measure to access memories.

The DNC also uses cosine similarity to retrieve memories. If \(\beta \in \mathbb{R} \) is a strength parameter, \(\mathbf{k} \in \mathbb{R}^W\), and \(\mathcal{D}(\mathbf{u},\mathbf{v})\) is the cosine similarity measure, then the probability that the DNC will access memory location \(i\) is given by:

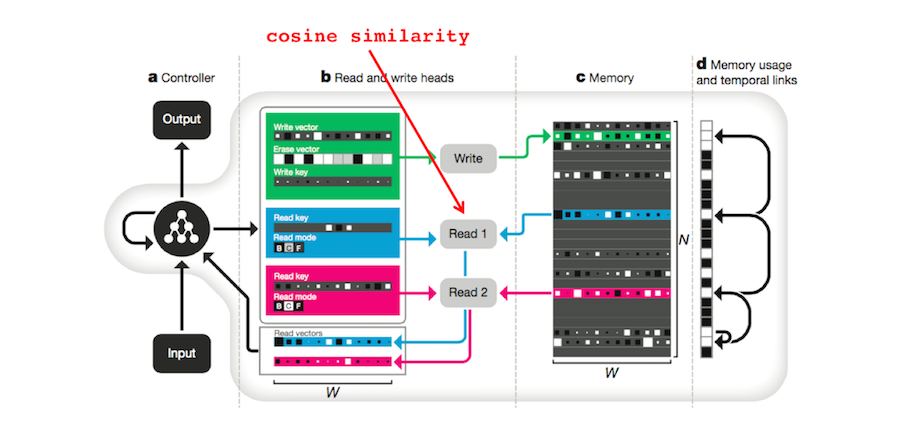
3. Search of Associative Memory (SAM). Kahana introduces the SAM model of human memory in Chapter 7 of Foundations of Human Memory ⁸. SAM was proposed by (Atkinson 1968)¹² to explain human free recall studies such as (Raaijmakers 1980)¹³, (Murdock 1962)¹⁴ and (Kahana 2008)¹⁵. As a dual-store model, it divides human memory into Short Term Storage (STS) and Long Term Storage (LTS).

The DNC has mechanisms for both STS and LTS. The DNC’s entire differentiable memory module is operated by a Long Short Term Memory (LSTM) RNN which has a form of short-term memory analogous to STS. The memory matrix \(M\) is, of course, analogous to LTS. The output of the DNC, \(\mathbf{y}_t\) is the sum of the RNN’s output, \(\mathbf{u}_t\) and a transformed representation of all the vectors read from the memory matrix \(W_r [\mathbf{r}_t^1; \ldots ;\mathbf{r}_t^R]\). In other words, the DNC produces responses based on both STS and LTS⁴:

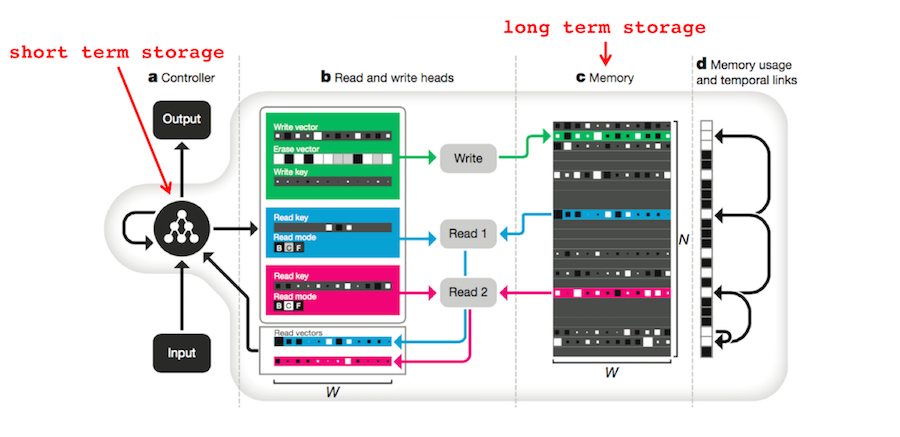
4. Temporal Context Model (TCM). Kahana introduces a second model of free recall called the Temporal Context Model (TCM)⁸. The idea is that when a human subject memorizes a sequence, the sequence itself determines context. In this model, context drives both memory storage and recovery.

How does the DNC use context to store and retrieve memories? First, the memory vectors themselves can contain context or point to related memories. Second, a temporal linkage matrix stores the order in which attribute vectors are written to memory. If \(\mathbf{p} \in \mathbb{R}^N\) is the precedence vector which represents “the degree to which location \(i\) was the last one written to”[10], \(\mathbf{w}^w \in \mathbb{R}^W\) is the normalized write weighting, and \(L \in \mathbb{R}^{N \times N}\) is the temporal linkage matrix, then \(L\) gets updated according to

According to the authors, ”\(L_t[i, j]\) represents the degree to which location \(i\) was the location written to after location \(j\)”⁴.

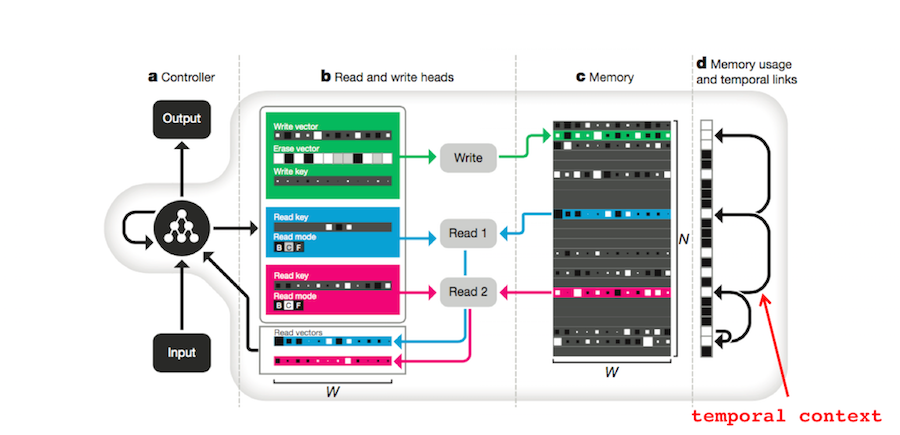
5. Serial recall. Chapter 8 of Foundations of Human Memory addresses serial recall models of human memory⁸. The two prevailing theories are chaining and positional coding (A and B respectively). If you are familiar with computer science, chaining basically says memory is a linked list and positional coding says memory is a regular list.

Models of serial recall. A. Chaining says that humans memorize series of items by creating memory links between adjacent items. B. Positional coding says that humans memorize series of items by storing their absolute locations within the sequence.

When explaining experimental data, chaining generally succeeds when positional coding fails and vice versa. The DNC can act analogously to both models depending on the situation. Show below are the DNC’s three read modes. They are content-based addressing ( \(\mathbf{c}_t^{r,i}\)), backwards traversal (\(\mathbf{b}_t^{r,i}\)), and forwards traversal (\(\mathbf{f}_t^{r,i}\)), respectively.

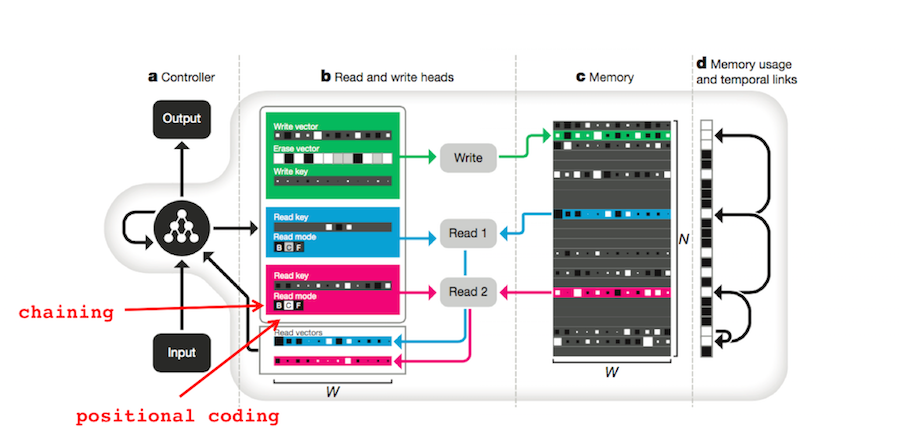
Free recall

“[Free recall] is a touchstone. If we can come to understand what is going on in free recall, then we can have some confidence that we understand the more basic [memory] processes” – B. B. Murdock, Human Memory

Testable? Hopefully I’ve convinced you that there are theoretical analogies between human memory and the DNC. What about experiments? According to the DNC Nature paper:

“Human ‘free recall’ experiments demonstrate the increased probability of item recall in the same order as first presented—a hippocampus-dependent phenomenon accounted for by the temporal context model, bearing some similarity to the formation of temporal links.”⁴ (my emphasis)

In case you’re unfamiliar with free recall, this term refers to a memory task wherein researchers present a subject with a sequence of items and then ask them to recall the items of the sequence in any order they wish. We just need to train the DNC on a free recall task and compare its responses to those of humans!

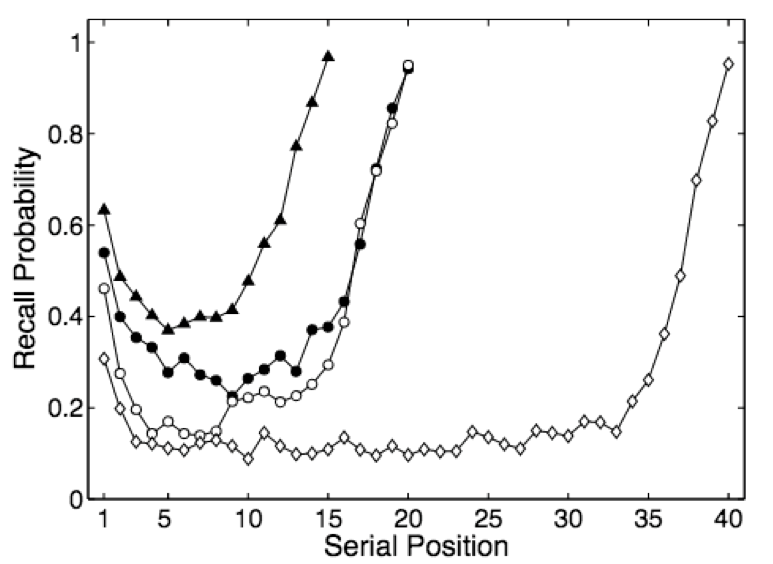
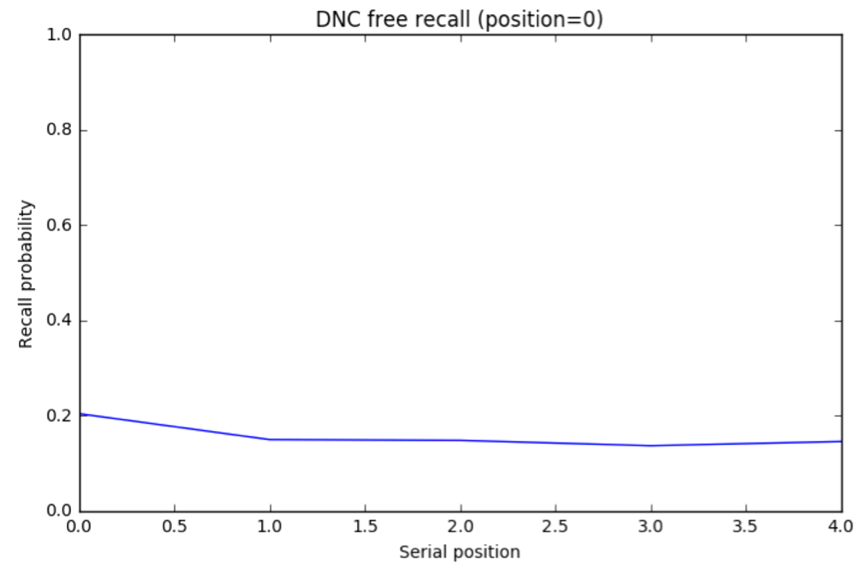
Human results. In human free recall experiments, subjects are more likely to respond with items near the beginning (primacy effect) or end (recency effect) of the sequence. The degree to which primacy and recency matter change according to sequence length, time delay, and other variables but human responses always exhibit these effects. Will the DNC?

Data for human subjects on the free recall task (Murdock 1962)[^fn14]

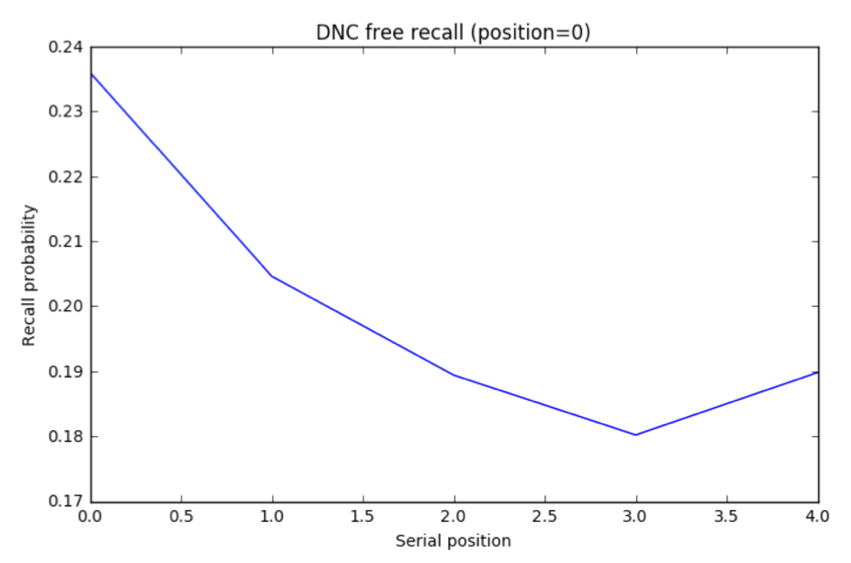
DNC results. I trained the DNC on a free recall task and ran 5000 trials (Jupyter notebook). The unscaled the distribution A of response probabilities exhibited primacy and recency effects similar to the human data. Choosing the same y axis as the plot for human subjects, B reveals that the DNC’s probability distribution is much more even.

The DNC exhibits both primacy and recency effects which supports the authors’ claim. But these effects, though present, are almost negligible compared to human subjects…our analogy is breaking down.

DNC free recall results show primacy and recency effects

Same scale as human free recall results

Where does the analogy break down?

“See that the imagination of nature is far, far greater than the imagination of man.” – Richard Feynman, Thoughts of a Citizen

Context. The DNC’s ability to store context is excellent. First, its temporal linkage matrix allows it to recall the exact order of write operations. Second, it can devote portions of the memory vectors themselves to context. For example, a given memory vector might contain both a memory and a ‘pointer’ pattern that tells the DNC how to access the next memory vector.

Context determines how we form memories, even in controlled laboratory settings

The DNC’s weakness lies in context-based recall. If it rains outside, your brain might remind you that you left your car window open. Maybe the context (rain) reminded you of how you left your coat outside last time it rained and it got soaked. What else could be damaged by the rain? The inside of your car! Now you remember that you left the window open. Since the DNC can only access memories via temporal links and direct content addressing, it cannot ‘traverse’ several memories like this in a single time step.

Backpropagation. Does the brain learn via backpropagation? Since neurons can only send information in one direction, the short answer is no. However, researchers have proposed a variety of ways the brain might work around the issue. Backpropagation weakens the DNC-brain analogy because the DNC uses backpropagation but the brain might not.

There are a few ways to get around the backpropagation issue. Geoffrey Hinton points to spike-time-dependent plasticity. A 2016 paper by neuroscientist Greg Wayne steps over the issue by arguing that the brain optimizes cost functions just like deep learning algorithms, regardless of the technical details. While these papers take research in the right direction, they don’t offer convincing proof one way or another.

Visualizing backpropagation in a 2-layer neural network (see my synthetic gradients post)

Forgetting. Forgetting \(\neq\) erasing. In fact, forgetting is a complex process which the brain modulates on many timescales. Sleep research indicates that humans consolidate memories during slow-wave sleep (SWS) and stabilize memories during random-eye-movement (REM) cycles (Rasch 2013)¹⁶. While sleep strengthens some memories, it weakens others. Since the DNC’s ability to forget is limited to an erase vector and an allocation gate, it cannot perform memory consolidation as humans do during sleep.

Neuron spike patterns in a young songbird (see (Rasch 2013)[^fn16])

I suspect that forgetting is the key reason the DNC performs differently from humans on the free recall task. Since humans forget items in the middle of free recall sequences more rapidly than the DNC, their recency and primacy effects are far greater.

Transfer learning. The final flaw with the DNC-brain analogy is transfer learning. The human brain can perform well on a wide range of memory tasks but the DNC, like most deep learning models, has to be retrained on each new task. For example, I had to train one DNC for the repeat-copy task and another for the free recall task.

There is a new area of deep learning research that aims to produce models that, like the brain, perform well across a large range of tasks. One model is the PathNet, which can learn to reuse its trained parameters on different tasks.

Transfer learning uses old knowledge to solve a new task (in this case, recognizing a dog)

Future directions

Reinforcement learning and memory. In reinforcement learning, an agent \(A\) exists in an environment \(E\). It has state $s$ from which it can make observations \(o\) and take actions \(a\) according to some policy \(\pi(s_t, o_t, a_{t-1})\). Through trial and error, the agent learns to behave according to policy \(\pi^*(s_t, o_t, a_{t-1})\), the policy which maximizes the total discounted reward (see intro blog post).

Reinforcement learning schema.

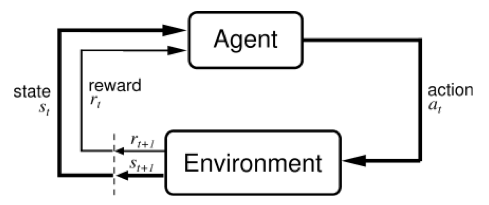
This framework can help us address some important issues in human memory. For example, how do humans decide what information to save to memory? If you’re constantly streaming ultra-high-definition sensory information from eyes, ears, taste buds, etc. you need to discard the vast majority of that information. Maybe memory should be framed as a reinforcement learning problem: an agent (the brain) chooses what information to store as memories \(M=[m_1, m_2,\dots,m_n]\) based on the probability \(p(R \vert M)\) that the memories will help it maximize its total discounted reward.

There’s a fair bit of evidence for this assertion. First, problems with working memory can impair reinforcement learning in humans. A 2016 paper explores memory in the context of reinforcement learning and demonstrates that memory consolidation improves reinforcement learning in dynamic environments. Finally, a recent review of reinforcement learning and episodic memory in humans claims that “the ubiquitous and diverse roles of memory in RL may function as part of an integrated learning system”.

Gershman and Daw propose an interaction between memory and reinforcement learning.

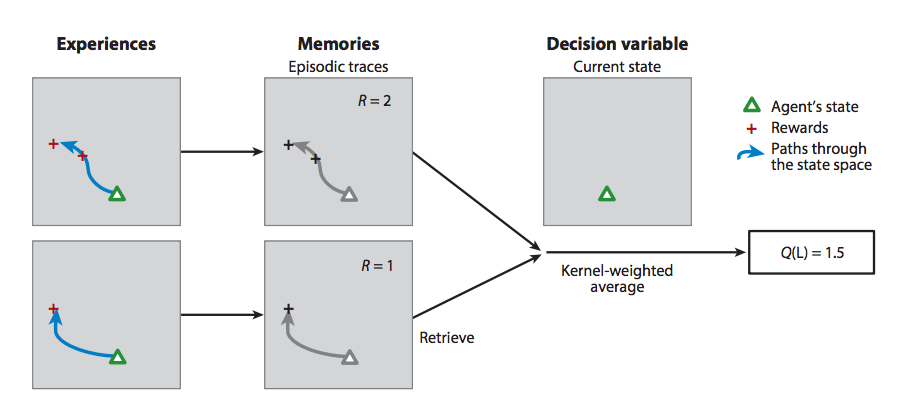
Researchers have already shown that the DNC performs well on reinforcement learning tasks. In fact, its large external memory might give it an advantage in transfer learning tasks. If this is the case, the DNC can help neuroscientists better understand how reward systems (e.g. dopamine pathways) might modulate memory systems (e.g. the hippocampus).

References.